Fix the Cycles

Fix the Cycles

You're given a directed weighted graph with 4 nodes (A, B, C, and D) and 6 edges, defined below:

• D→A       has weight a
• A→ B              has weight b
• B→C  has weight c
• C→D  has weight d
• A→C  has weight e
• B→D  has weight f

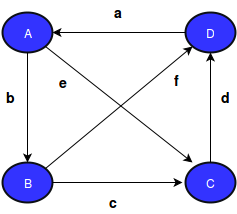
The total weight of a simple cycle is the sum of its edge weights (e.g.: A→C→D→A has a total weight of e+d+a). If the total weight is negative, it's called a negative cycle.

Given edge weights a, b, c, d, e, and f, find some minimum non-negative integer (p) that, when added to one single edge weight in the graph, will get rid of any negative cycles.

Input Format

A single line containing 6 space-separated integers: a, b, c, d, e, and f, respectively.

Constraints

• −20≤a,b,c,d,e,f≤20

Output Format

Print the minimum value of p; if no non-negative p will eliminate the negative cycle, print −1.

Sample Input

2 -5 0 1 1 1

Sample Output

2

Explanation

Adding 2 to b (the weight of edge A→B ) will remove the negative cycle.

Runtime Analysis:

Given that the graph is limited in size to only nodes: A, B, C, D, E, F and the edges are predefined, as long as we come up with a reasonable approach, runtime shouldn't be an issue here. In the worst case, we will take each possible path and our runtime will be equal to the number of cycle. Our solution given is in O(n) where n is the longest cycle in the graph.

Runtime: O(n)

Algorithmic Approach:

This problem can be solved using some basic logic. 

The only cycles in this problem are:

a, b, c, d

a, b, f

d, a, e

You could argue that there are more cycles including: 

(a, b, c, d, a, e, d) with (a, e, d) repeating

(c, d, a, b, f, a, b) with (f, a, b) repeating

But these cycles can be broken down to a subset of sequences above:

(a, b, c, d, a, e, d) => (a, b, c, d) + (d, a, e)

(c, d, a, b, f, a, b) => (a, b, c, d) + (a, b, f)

So, we just need to find an integer to make all 3 cycles above non negative.

Notice that all the cycles above have 1 common edge:

Edge a

Since we can only modify 1 edge, the greedy approach tells us that we should increase edge a, so that we are increasing the values of all 3 cycles.

The code then becomes relatively simple: 

1. Find the smallest cycle sum
2. If positive, print 0
3. Else, multiply the result by -1

Furthermore, since all cycles share edge a, there will always exist a non negative p to eliminate all negative cycles. 

Java Code: 

import java.io.*;
import java.util.*;
import java.text.*;
import java.math.*;
import java.util.regex.*;

public class Solution {

    public static void main(String[] args) {
        /* Enter your code here. Read input from STDIN. Print output to STDOUT. Your class should be named Solution. */
        
        Scanner sc = new Scanner(System.in);
        String line = sc.nextLine();
        
        String [] arr = line.split(" ");
        
        int a = Integer.parseInt(arr[0]);
        int b = Integer.parseInt(arr[1]);
        int c = Integer.parseInt(arr[2]);
        int d = Integer.parseInt(arr[3]);
        int e = Integer.parseInt(arr[4]);
        int f = Integer.parseInt(arr[5]);

        int s = Math.min(Math.min(a+b+f, b+c+d+a), d+a+e);
        
        if(s >= 0){
            System.out.println(0);
            return;
        }
        else{
            a += (-1 * s);

            if(Math.min(Math.min(a+b+f, b+c+d+a), d+a+e) < 0){
                System.out.println(-1);
            }
            else{
                System.out.println((-1 * s));
            }
        }
    }
}